ESG guidance and artificial intelligence support for power systems analytics in the energy industry

May 18, 2024

34 13 minutes read

Untitled design6 — 1716026920 41598 2024 61491 Fig1 HTML.png

Application of ESG framework in power system analysis

ESG framework plays a vital role in the energy industry, covering three aspects of environment, society and governance, and has become a key indicator for enterprises and industries to evaluate sustainability and social responsibility^21,22. In the energy industry, especially in power system analysis, ESG framework plays a guiding and evaluating role, as displayed in Table 1.

Table 1 Application of ESG framework in power system.

In Table 1, the application of ESG framework in power system is mainly reflected in three aspects: environment, society and governance. In terms of environment, ESG framework pays attention to sustainability by evaluating the impact of power system on the environment. Through the ESG framework, energy companies can more comprehensively evaluate the environmental impact of their power production methods, thus promoting a more environmentally friendly and sustainable energy production model. In the social aspect, ESG framework also pays attention to the impact of power system on society, such as employee welfare, the impact of local communities and social responsibility. In power system analysis, social indicators may include the implementation of social responsibility projects, employee welfare and safety measures. By considering these factors, the social sustainability of power system can be evaluated and the development of social justice and responsibility can be promoted. In terms of governance, this involves the effectiveness of regulatory compliance and decision-making transparency. Through these indicators, the good governance of power system can be evaluated.

Therefore, the application of ESG framework in power system analysis not only helps to evaluate the sustainability and environmental friendliness of power system, but also promotes the development of energy industry towards more social responsibility and governance norms. In order to support the more standardized and effective operation of the power system in the energy industry, the deep learning algorithm is further introduced by this study to anticipate the power demand and fault detection in the power system.

Application of deep learning to power load demand forecasting and analysis

This study uses a deep learning algorithm to predict power demand, coordinate the operation of various components, and guarantee the security and balance of the power system to analyze the energy industry’s power system and lessen the high fluctuation and uncertainty of the power grid load brought on by residents’ behavior.

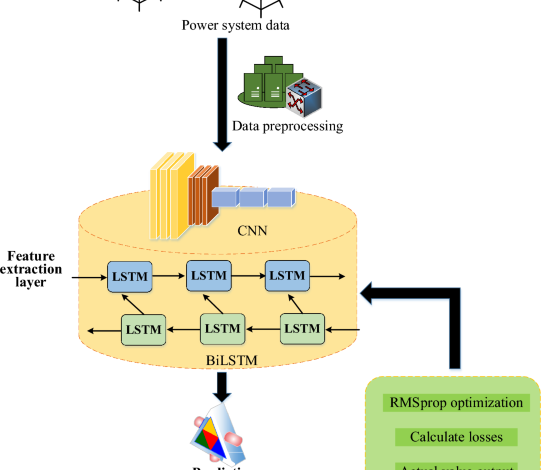
The one-dimensional nature of power load data significantly restricts the neural network’s capacity to extract the full range of information from power load series. Implicit qualities include the link between power load data and time series data continuity. CNN²³ has the ability to map one-dimensional data into multi-dimensional data, completely utilize the information contained in power load series, and enhance the features of restricted data. CNN is therefore able to adequately represent the regional features of power load data. Meanwhile, power load data sequentially records power consumption based on a predetermined time interval and sampling frequency. Therefore, this study further introduces BiLSTM algorithm²⁴ to extract the features of power load data. Eventually, a CNN-BiLSTM-based model structure for power load demand forecasting is built, as seen in Fig. 1, including input, feature extraction, prediction, output, and network optimization layers.

In Fig. 1, the power load demand forecasting model mainly consists of two parts: feature extraction and data forecasting. After preprocessing the data in the power system, CNN extracts the feature information sequence from the pre-processed time series. CNN module uses two convolution layers and ReLU as the activation function to make the network more trainable.

Brief introduction and working principle of CNN-BiLSTM model

CNN-BiLSTM model combines CNN and BiLSTM to process time series data, such as the data in power load demand forecasting. Among them, CNN model consists of convolution layer, pooling layer, and activation function, which can effectively extract features from one-dimensional data. In power load demand forecasting, CNN is used to transform one-dimensional power load data into multi-dimensional data to better capture the spatial characteristics of the data. Through convolution operation and activation function, CNN can extract key features from data, such as load fluctuation and trend. In power load demand forecasting, CNN model is used for feature extraction, which transforms the original one-dimensional power load data into multi-dimensional feature sequence, so that the subsequent forecasting model can better understand and process the data.

BiLSTM model is composed of forward and backward LSTM networks, which captures the context of sequence data respectively. BiLSTM can capture the long-term dependence in sequence data to better understand the time dynamic characteristics of data. Through the forward and backward LSTM networks, BiLSTM can consider the data of the current moment and the data of the past moment at the same time to predict the future trend. In power load demand forecasting, BiLSTM model is used for sequence forecasting, receiving the feature sequence extracted from CNN model, and forecasting the future power load demand by learning the time dependence of sequence data.

CNN-BiLSTM model combines the feature extraction ability of CNN with the sequence modeling ability of BiLSTM, and makes full use of the spatial and temporal dynamic characteristics in time series data. Through this integration, the model can predict the future power load demand more accurately and improve the accuracy and stability of the prediction. The model integrating CNN and BiLSTM can better capture the spatial and temporal characteristics of data in power load demand forecasting and improve the accuracy of forecasting. The features are extracted by CNN model and passed to BiLSTM model for sequence modeling. The model can better understand the complexity of power load data and make more reliable predictions. In a word, by integrating the advantages of CNN and BiLSTM, CNN-BiLSTM model can process time series data more effectively, and improve the accuracy and stability of forecasting, thus playing an important role in energy industry.

When using CNN network to extract the features of the power data in the original power system, preprocess it first. If the original power data is as shown in Eq. (1):

$$\Phi = \left\{ {\varphi_{1} ,\varphi_{2} , \ldots ,\varphi_{N} } \right\}.$$

(1)

Let T be the length of time series, that is, predict the ith point and take the previous T points as input, then the data set $\Psi$ can be expressed as Eq. (2):

$$\Psi = \left\{ {\Psi_{1} ,\Psi_{2} , \ldots ,\Psi_{n – T} } \right\}.$$

(2)

$\Psi_{i}$ can be expressed as Eq. (3):

$$\Psi_{i} = \left\{ {\varphi_{j – L} ,\varphi_{j – L + 1} , \ldots ,\varphi_{j – 1} } \right\},\;1 \le i \le n – L,\;j = i + L,i,j \in N.$$

(3)

Equation (4) serves as the conversion function, and the data is processed using the min–max standardization method to increase the model algorithm’s operational efficiency.

$$x_{j}^{\prime} = \frac{{x_{i} – x_{\min } }}{{x_{\max } – x_{\min } }}.$$

(4)

$x_{i}$ refers to raw data and $x_{j}{\prime}$ refers to standardized data.

A dropout layer is added between CNN feature extraction block and BiLSTM sequence prediction to prevent over-fitting. Then, BiLSTM network is used to effectively process the input characteristic information sequence data, which can capture the dependence between data information in power system.

The features $x_{t}$ and $h_{t – 1}$ of data information in the power system are input into the BiLSTM model, and the input data are obtained by sigmoid function, and the coefficients $f_{t} ,i_{t}$ are input by activation function, and the temporary unit variable $\tilde{c}_{t}$ is obtained. The calculation process is shown in Eqs. (5)–(7):

$$f_{t} = \delta \left( {\left[ {W_{f} \cdot \left[ {h_{t – 1} ,x_{t} } \right] + b_{f} ,W_{f}^{\prime} \cdot \left[ {h_{t – 1}^{\prime} ,x_{t} } \right] + b_{f}^{\prime} } \right]} \right),$$

(5)

$$i_{t} = \delta \left( {\left[ {W_{i} \cdot \left[ {h_{t – 1} ,x_{t} } \right] + b_{i} ,W_{i}^{\prime} \cdot \left[ {h_{t – 1}^{\prime} ,x_{t} } \right] + b_{i}^{\prime} } \right]} \right),$$

(6)

$$\tilde{C}_{t} = \tanh \left( {\left[ {W_{C} \cdot \left[ {h_{t – 1} ,x_{t} } \right] + b_{c} ,W_{c}^{\prime} \cdot \left[ {h_{t – 1}^{\prime} ,x_{t} } \right] + b_{c}^{\prime} } \right]} \right).$$

(7)

$\sigma$ and tanh are activation functions, and the former is sigmoid function. $W_{f} ,W_{i} ,W_{C} ,W_{o}$ are weight parameters. $h_{t – 1}$ refers to the output of the previous neuron. $C_{t}$ refers to the cell state at time t. $h_{t}$ refers to the hidden layer output at time t, and b refers to the bias vector. Then, the hidden state h_t at t can be expressed as Eqs. (8)–(10):

$$\vec{h}_{t} = \overrightarrow {LSTM} \left( {\vec{W}_{t} ,\vec{h}_{t – 1} ,\vec{b}_{t} ,\vec{c}_{t – 1} } \right),$$

(8)

$$\mathop{h}\limits^{\leftarrow} _{t} = \overleftarrow {LSTM} \left( {\mathop{W}\limits^{\leftarrow} _{t} ,\mathop{h}\limits^{\leftarrow} _{t – 1} ,\mathop{b}\limits^{\leftarrow} _{t} ,\mathop{c}\limits^{\leftarrow} _{t + 1} } \right),$$

(9)

$$h_{t} = \left[ {\vec{h}_{t} ,\mathop{h}\limits^{\leftarrow} _{t} } \right].$$

(10)

W and b respectively represent the relative weights of the door unit and the memory cell. c_t and h_t respectively represent the state of the memory cell and the hidden state of LSTM at t. → and ← represent forward data feature prediction and reverse data feature prediction respectively.

In the process of back propagation, the parameters in the model should be updated in the direction of the fastest gradient decline. Assume that the network parameter is $\theta$, the learning rate is $\eta$. The function represented by the network is $J\left( \theta \right)$. The maximum gradient of the function to $\theta$ at this time can be expressed as $\nabla_{\theta } J\left( \theta \right)$, so the updating equation of parameters can be expressed as Eq. (11):

$$\theta = \theta – \eta \nabla_{\theta } J\left( \theta \right).$$

(11)

In order to further optimize the problem that the loss function has too large swing amplitude in the update of the model and accelerate the convergence speed of the function, RMSProp algorithm uses the differential square weighted average for the gradient of weight W and offset b, as shown in Eqs. (12)–(15):

$$s_{dW} = \beta s_{dW} + \left( {1 – \beta } \right)dW^{2} ,$$

(12)

$$s_{db} = \beta s_{db} + \left( {1 – \beta } \right)db^{2} ,$$

(13)

$$W = W – \alpha \frac{dW}{{\sqrt {s_{dW} } + \varepsilon }},$$

(14)

$$b = b – \alpha \frac{db}{{\sqrt {s_{db} } + \varepsilon }}.$$

(15)

$s_{dW}$ and $s_{db}$ refer to the weighted average of exponential squares initialized to zero, respectively, and $\beta$ refers to momentum.

In this model, the pseudo code of CNN-BiLSTM algorithm applied to power load demand forecasting is shown in Fig. 2.

In Fig. 2, firstly, CNN-BiLSTM algorithm receives raw power data as input, and outputs the prediction result of power load demand. In the data preprocessing stage, the original data is preprocessed to prepare for the subsequent feature extraction. Then, CNN model is used to extract features from the preprocessed data, and a CNN feature extraction function is defined to ensure that the model can effectively extract important spatial features from the data. Then, BiLSTM model is used to predict the sequence of features extracted from CNN to capture the time dynamic features in the data, and this process is realized by the defined BiLSTM sequence prediction function. Finally, RMSProp algorithm is used to train and optimize the model to improve the performance and prediction accuracy of the model. After the whole process, the algorithm gives the prediction results of future power load demand. Through this algorithm flow, CNN-BiLSTM model can be effectively applied to accurately predict the power load demand, which provides important support and guidance for the management and operation of the energy industry.

Application of DBN in power system fault prediction and analysis

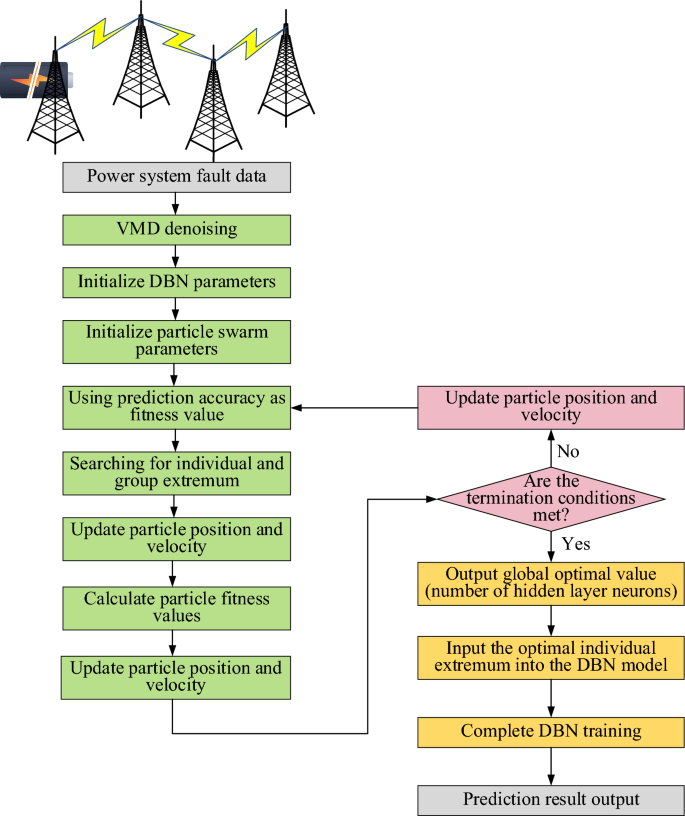
At present, with the concept of smart grid put forward, the establishment of intelligent information operation and maintenance platform store a lot of data, and the large-scale access of distributed power sources increases the nonlinearity and uncertainty of data, which makes the fault analysis of power system more difficult. Aiming at the fault analysis of power system under the new situation, this study proposes a power grid fault diagnosis model based on PSO algorithm and DBN, as shown in Fig. 3.

In Fig. 3, firstly, power system fault data is input, and the input data is denoised by Variational Mode Decomposition (VMD)²⁵. Then, the parameters of DBN²⁶ and PSO algorithm²⁷ are initialized. The model takes the accuracy of fault prediction as the fitness function of PSO algorithm to guide it to search for individual and global optimal solutions. PSO algorithm constantly updates the position and velocity of particles to converge towards the optimal solution step by step. If the requirements are satisfied, the global optimal value—which denotes the ideal number of neurons in the hidden layer—is produced by iterative evaluation. In the event that the termination condition is not satisfied, the PSO algorithm will go on finding the optimal architecture while updating the particle’s position and speed. The optimal individual value, or the ideal number of neurons in the hidden layer, is sent into the DBN model for training once the termination condition is satisfied. Finally, DBN training is completed and the identification results of power grid faults is output.

In this model, the fault parameter estimation is defined as Eq. (16):

$$\hat{\beta }_{k – 1,k}^{i} = g\left( {\overline{y}_{k} ,W_{k}^{i} ,V_{k}^{i} } \right).$$

(16)

$\hat{\beta }_{k – 1,k}^{i}$ is the i-th fault parameter when calculating k-1 at time k. $W_{k}^{i} ,V_{k}^{i}$ are the weight matrix of the output layer and hidden layer of the i-th DBN. $\overline{y}_{k}$ is the input vector of the DBN, and g is the nonlinear mapping realized by the DBN. During training, the Lyapunov function²⁸ changes as shown in Eq. (17):

$$\Delta L_{k} = \frac{1}{2}\left( {e_{k + 1}^{2} – e_{k}^{2} } \right).$$

(17)

$e_{k}^{{}}$ refers to learning error. Let $G_{k} = \partial J_{k} /\partial W_{k} ,G_{k\max } = \mathop {\max }\limits_{k} ||G_{k} ||$. Because of $\eta_{1} = \eta_{w} G_{k\max }^{2}$, the Eq. (18) is defined:

$$\lambda = \frac{1}{2}||G_{k} ||^{2} \eta_{1} \left( {2 – \eta_{1} ||G_{k} ||^{2} } \right).$$

(18)

If the condition satisfying the convergence of the DBN is $\Delta L_{k} < 0$, then $\lambda > 0$. The following equation can be obtained from Eq. (18).

$$0 < \eta_{1} < \frac{2}{{||G_{k} ||^{2} }}.$$

(19)

If Eq. (19) is satisfied in the DBN, the network model can be kept stable and convergent, thus the state and output of the power system can be predicted.

The fault diagnosis and prediction framework can be divided into the following steps:

(1)

Data preprocessing. Input power system fault data, which may include power grid operation status, equipment sensor data, etc. Variational Modal Decomposition (VMD) is used to denoise the data, so as to reduce the interference noise in the data and improve the robustness and accuracy of the subsequent model.
(2)

Model initialization. Particle swarm optimization (PSO) is used to initialize the parameters of deep belief network (DBN) and PSO. DBN is a neural network model with multiple hidden layers, which is used for fault diagnosis and prediction.
(3)

PSO process. PSO algorithm takes the accuracy of fault prediction as the fitness function, and constantly updates the position and speed of particles to find the optimal parameter configuration of neural network. Through iterative optimization, PSO algorithm guides particles to search in the direction of global optimal solution.
(4)

PSO algorithm termination conditions. PSO algorithm will continue to iterate and update until the termination conditions are met, such as the maximum number of iterations, accuracy requirements or other preset conditions.
(5)

Once the PSO algorithm meets the termination conditions, it outputs the global optimal value, which represents the optimal number of neurons in the hidden layer. This value will be used as a key parameter for subsequent DBN model training.
(6)

DBN model training. The optimal number of hidden layer neurons determined by PSO algorithm will be used as the hidden layer configuration of DBN model, and then the DBN model will be trained. This step may involve supervised learning with fault data, so that the model can accurately identify power grid faults.
(7)

Output of fault diagnosis results. After completing the training of DBN model, the model will be used to identify and predict power grid faults. Finally, through this process, the identification results of power grid faults are output, which provides guidance for subsequent fault treatment and maintenance.

This framework integrates data preprocessing, PSO and DBN to effectively diagnose and predict power grid faults and improve the accuracy and robustness of power system faults.

Experimental analysis

In order to analyze the performance of the power load demand forecasting model based on CNN-BiLSTM, the smart meter data of XX community in Xi’an from October 2021 to October 2022 are collected. The original power load data is collected every 6 s by the home smart meter, but this study analyses and forecasts the 5-min power load data and needs to convert the data unit. The load data is converted into electricity consumption within 5 min, and then the data are integrated, and 36,105 power data are obtained after integration. According to a 7:3 ratio, power statistics are split at random into training and test sets. The model makes use of a number of Python modules and the TensorFlow simulation framework. There are 100 iterations and a batch size of 100 in the particular super parameter settings. The random gradient descent algorithm is utilized to optimize the loss function, with a starting learning rate of 0.001. The model techniques presented by CNN, BiLSTM, LSTM²⁹, and Ahmadian et al. are utilized to evaluate the model’s performance in this study using three different metrics: root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE).

Furthermore, the performance of the power grid fault diagnosis model based on PSO algorithm and DBN is evaluated. The simulation experiment is completed on an Inter Core i7-9750H personal computer with a single CPU of 2.6 GHz, 16 GB of memory and 64-bit operating system. Because the accuracy of model identification will change with the number of hidden layers, DBN models with hidden layers of 1, 2, 3, 4 and 5 are built respectively. The number of neurons in each layer is set to 200, the number of iterations is set to 100, the loss function is cross entropy, the learning rate adopts random gradient descent algorithm, and the initial learning rate is set to 0.001. The improved 10 kV distribution network model of IEEE13 nodes is established, the arc fault module is analyzed, and the early fault model is completed. Half-cycle early fault, multi-cycle early fault, fixed impedance grounding, motor start-up and load switching are respectively set, and the load of each fault branch is respectively set to light load, heavy load, and full load. When the motor is started, three groups of situations with different power levels are set according to the power level of the motor. The switching time of capacitors is set to 9 random values in a cycle, and 12 groups of capacitors with different sizes are set. According to the above simulation conditions, the obtained data are parameterized, and a total of 8517 groups of samples are obtained. The training set consists of 70% data samples of various state types, and the remaining 30% samples constitute the test set. Compared with the model algorithms proposed by DBN, General Regression Neural Network (GRNN)³⁰ and Hong et al. in terms of accuracy and training time.

Source

May 18, 2024

34 13 minutes read