Machine learning optimization for hybrid electric vehicle charging in renewable microgrids
In the realm of energy management, the primary responsibility of the operator revolves around ensuring the dependable and secure supply of energy to electrical consumers, all while striving to minimize expenses . As a result, the objective function combines operational costs and technical expenditures, manifesting in the following manner Minimize the total cost, considering both operating and technical costs:
$$\begin{aligned} \begin{aligned}{}&\text {Minimize the total cost, considering both operating and technical costs:} \\&\text {MinimizeCost} = \\&\sum _{\forall \omega _b} \sum _{\forall \tau _t} \left( \rho _G \cdot \text {OperatingCost}_{G,\omega _b,\tau _t} + \rho _M \cdot \text {OperatingCost}_{M,\omega _b,\tau _t} \right. \\&\left. + \rho _{MPHEV} \cdot \text {EVChargingCost}_{\omega _b,\tau _t} + \rho _{MR} \cdot \text {TechnicalCost}_{\omega _b,\tau _t} \right) \\&+ \lambda \cdot \text {PenaltyCost} \end{aligned} \end{aligned}$$
(22)
Operating cost constraints for distributed generators (DGs)
Active power limits
$$\begin{aligned} P_{\text {min},m,t} \le P_{G,m,t} \le P_{\text {max},m,t} \quad \forall m \in \Omega _B, \forall t \in \Omega _T \end{aligned}$$
(23)
Reactive power limits
$$\begin{aligned} Q_{\text {min},m,t} \le Q_{G,m,t} \le Q_{\text {max},m,t} \quad \forall m \in \Omega _B, \forall t \in \Omega _T \end{aligned}$$
(24)
Ramp Up/Down limits
$$\begin{aligned}{} & {} P_{G,m,t} – P_{G,m,t-1} \le R_{U,m} P_{G,m,t-1} \quad \forall m \in \Omega _B, \forall t \in \Omega _T \end{aligned}$$
(25)
$$\begin{aligned}{} & {} P_{G,m,t-1} – P_{G,m,t} \le R_{D,m} P_{G,m,t} \quad \forall m \in \Omega _B, \forall t \in \Omega _T \end{aligned}$$
(26)
Constraints related to energy storage systems
Minimum charging time
$$\begin{aligned} T_{\text {Ch}} \ge CTS(y_{\text {Ch},m,t} – y_{\text {Ch},m,t-1}) \quad \forall m \in \Omega _{\text {BS}}, \forall t \in \Omega _T \end{aligned}$$
(27)
Minimum discharging time
$$\begin{aligned} T_{\text {Disch}} \ge DTS(y_{\text {Disch},m,t} – y_{\text {Disch},m,t-1}) \quad \forall m \in \Omega _{\text {BS}}, \forall t \in \Omega _T \end{aligned}$$
(28)
Charging and discharging mode constraints
$$\begin{aligned} y_{\text {Ch},m,t} + y_{\text {Disch},m,t} \le 1 \quad \forall m \in \Omega _{\text {BS}}, \forall t \in \Omega _T \end{aligned}$$
(29)
Constraints related to adjustable load demand
$$\begin{aligned} PAD_{zAD,m,t} \le PD_{m,t} \le PAD_{zAD,m,t} \quad \forall m \in \Omega _{BAD}, \forall t \in \Omega _T \end{aligned}$$
(30)
Constraints related to DGs and energy storage systems
Minimum up and down time limits for DGs
$$\begin{aligned}{} & {} T_{G,\text {on}} \ge UTG(x_{G,m,t}) \quad \forall m \in \Omega _{BG}, \forall t \in \Omega _T \end{aligned}$$
(31)
$$\begin{aligned}{} & {} T_{G,\text {off}} \ge DTG(x_{G,m,t}) \quad \forall m \in \Omega _{BG}, \forall t \in \Omega _T \end{aligned}$$
(32)
Constraints for total energy stored in batteries
Total energy stored in batteries
$$\begin{aligned} CS_{m,t}= & {} CS_{m,t-1} + \eta _{\text {Disch}} P_{\text {Disch},m,t} – \eta _{\text {Ch}} P_{\text {Ch},m,t} \quad \forall m \in \Omega _{\text {BS}}, \forall t \in \Omega _T \end{aligned}$$
(33)
$$\begin{aligned}{} & {} C_{mS,t} \le CS_{m,t} \le C_{mS,t} \quad \forall m \in \Omega _{\text {BS}}, \forall t \in \Omega _T \end{aligned}$$
(34)
Constraints for bus voltage and main grid power limits
Bus voltage limits
$$\begin{aligned} V_{m,t} \le V \le V_{m,t} \quad \forall m \in \Omega _B, \forall t \in \Omega _T \end{aligned}$$
(35)
Main grid power limits
$$\begin{aligned} -P_M \le P_{M,m,t} \le P_M \quad \forall m \in \Omega _B, \forall t \in \Omega _T \end{aligned}$$
(36)
Constraints for reconfiguration using remote switches
Binary variables indicating the status of lines
$$\begin{aligned} 0 \le I_{mLn,t} \le I_{LmLn,t} \quad \forall m,n \in \Omega _L, \forall t \in \Omega _T \end{aligned}$$
(37)
$$\begin{aligned} \sum _{\begin{array}{c} mn \in \Omega _L \\ m\in \Omega _B \end{array}} I_{mLn,t} = 1 \quad \forall m \in \Omega , \forall t \in \Omega _T \end{aligned}$$
(38)
$$\begin{aligned}{} & {} 0 \le \theta _{mn,t} \le w_{mn,t} \quad \forall mn \in \Omega , \forall t \in \Omega _T \end{aligned}$$
(39)
$$\begin{aligned}{} & {} P_{\text {min},m,t} \le P_{G,m,t} \le P_{\text {max},m,t} \quad \forall m \in \Omega _B, \forall t \in \Omega _T \end{aligned}$$
(40)
Electric vehicle
$$\begin{aligned} 0&\le P_{EV,\omega _b,\tau _t} \le P_{\text {max, EV},\omega _b} \quad \forall \omega _b, \forall \tau _t \end{aligned}$$
(41)
Voltage limit
$$\begin{aligned} V_{\text {min},m,t}&\le V_{m,t} \le V_{\text {max},m,t} \quad \forall m \in \Omega _B, \forall t \in \Omega _T \end{aligned}$$
(42)
Current limit
$$\begin{aligned} I_{\text {min},\omega _l,\tau _t}&\le I_{\omega _l,\tau _t} \le I_{\text {max},\omega _l,\tau _t} \quad \forall \omega _l, \forall \tau _t \end{aligned}$$
(43)
$$\begin{aligned} \text {PenaltyCost}&\ge \sum _{\text {violations}} \text {PenaltyWeight} \cdot \text {Deviation} \end{aligned}$$
(44)
The charging patterns of Hybrid Electric Vehicles (HEVs) are influenced by a multitude of factors, including market penetration, State of Charge (SoC), charging duration, and more. To seamlessly integrate HEVs into the system, it is crucial to precisely define these uncertain parameters, thereby reducing inherent variability. This study employs the Support Vector Regression (SVR) method to predict the overall charging demands of HEVs.
From a technical perspective, HEVs are versatile in their ability to draw energy from either traditional gasoline or electricity sources. Figure 2 offers an overview of the fundamental components of HEVs35. In this representation, the cylindrical component signifies fuel storage, emphasizing that HEVs operate by harnessing power from both electrical and fossil fuel sources. To extend this discussion to microgrid energy management, it’s essential to consider how constraint parameters are selected to optimize system performance and stability.In this study, the selection of constraint parameters was methodically driven by a deep understanding of the microgrid’s unique characteristics and operational needs. The research team began by closely examining the size and complexity of the microgrid, alongside the types of distributed energy resources (DERs) integrated within it. This analysis allowed for the tailoring of constraints to match the capabilities of the specific DERs, ensuring they could effectively meet demand without jeopardizing system stability. For instance, when defining the Active and Reactive Power Limits for distributed generators (DGs), meticulous consideration was given to each generator’s capacity and operational behavior. By aligning limits with the capabilities of these generators, the aim was to strike a balance between meeting demand and preventing system overload. The approach to Energy Storage System parameters involved a thorough assessment of storage capacity and anticipated load fluctuations. By carefully selecting charging and discharging times, the goal was to optimize energy storage utilization while minimizing disruptions to grid operations. Adjustable Load Demand constraints were chosen to provide the desired level of flexibility in managing load demands, all while ensuring compatibility with available generation capacity. This involved a nuanced understanding of the microgrid’s load profile and resource capabilities. Similarly, Bus Voltage and Main Grid Power Limits were tailored to maintain voltage stability and manage power flow within acceptable thresholds, accounting for the microgrid’s specific infrastructure and operational needs. Finally, parameters governing Reconfiguration Using Remote Switches were designed to enhance the microgrid’s reliability and resilience, enabling efficient adaptation to changing conditions
Power flow analysis and voltage stability
The power flow equations within a microgrid are vital for ensuring reliable operation and voltage stability. They are typically addressed using iterative methods such as the Newton-Raphson approach. One key equation is the power balance equation at each node, which maintains overall power balance by equating injected and withdrawn power. Mathematically, this equation ensures that the sum of injected active and reactive power equals the sum of withdrawn power at each node:
$$\begin{aligned} P_{i\text {injected}} – P_{i\text {withdrawn}} + j(Q_{i\text {injected}} – Q_{i\text {withdrawn}}) = 0 \end{aligned}$$
(45)
where \(P_{i\text {injected}}\) and \(Q_{i\text {injected}}\) represent the injected active and reactive power at node i, and \(P_{i\text {withdrawn}}\) and \(Q_{i\text {withdrawn}}\) represent the withdrawn active and reactive power at node i. Another critical aspect of power flow analysis is the relationship between voltage magnitudes and phase angles at neighboring nodes. This relationship governs power flow across transmission lines and ensures voltage stability within the system. Mathematically, the relationship between voltage magnitudes and phase angles at node i and its neighboring node j can be expressed as:
$$\begin{aligned} V_i\angle \theta _i – V_j\angle \theta _j = Z_{ij}(I_{ij}) \end{aligned}$$
(46)
where \(V_i\) and \(V_j\) are the voltage magnitudes at nodes i and j, \(\theta _i\) and \(\theta _j\) are the phase angles at nodes i and j, \(Z_{ij}\) is the impedance of the transmission line connecting nodes i and j, and \(I_{ij}\) is the complex current flowing from node i to node j. The Newton-Raphson method is employed to iteratively solve these nonlinear equations, adjusting node voltages until power mismatches meet acceptable criteria. By doing so, it ensures balanced power distribution and maintains voltage stability within acceptable thresholds, addressing operating security concerns. The study’s methodology addresses challenges related to power flow constraints, including fluctuating demand and intermittent renewable energy sources, by integrating advanced optimization techniques into the Newton-Raphson algorithm. By doing so, the study aims to enhance the resilience and efficiency of microgrid operation in the face of dynamic energy demands and environmental variability. In the context of microgrid energy management, the selection of parameters for power flow analysis and voltage stability is crucial for ensuring reliable operation and system resilience. When determining these values, various factors specific to the microgrid’s characteristics and operational requirements must be considered. Firstly, the impedance values (\(Z_{ij}\)) of transmission lines connecting different nodes within the microgrid are chosen based on factors such as line length, material, and loading conditions. These values directly influence the relationship between voltage magnitudes and phase angles, as described by Equation (46). Selecting appropriate impedance values ensures efficient power transfer and voltage stability across the microgrid. Additionally, the criteria for acceptable power mismatches and voltage thresholds are established to maintain system stability under varying operating conditions. These criteria are determined based on factors such as load variations, renewable energy generation fluctuations, and grid disturbances. Optimizing these criteria involves striking a balance between system stability and operational efficiency. Furthermore, the selection of parameters for the Newton-Raphson method, such as convergence criteria and iteration limits, plays a crucial role in the accuracy and efficiency of power flow analysis. Setting appropriate values for these parameters ensures that the iterative solution converges to a stable solution within a reasonable computational time. The impact of these parameter selections on overall performance is significant. For example, overly conservative impedance values may result in excessive voltage drops and power losses, leading to reduced system efficiency. Conversely, overly aggressive convergence criteria may increase computational burden without significant improvement in accuracy.
Limitations
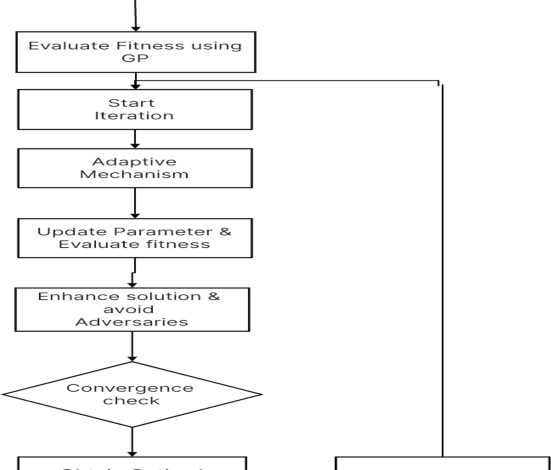
While the proposed methodology represents a significant advancement in microgrid management, it is essential to acknowledge certain limitations inherent in its components. One potential limitation arises from the computational complexity associated with solving power flow equations using the Newton-Raphson method. Although effective for voltage stability analysis and power flow optimization in steady-state conditions, the iterative nature of this approach demands significant computational resources, particularly in large microgrid networks or real-time applications. Despite advancements in computing technology, managing these computational demands remains a consideration for practical implementation. Similarly, the Krill algorithm’s sensitivity to parameter settings and its reliance on underlying assumptions pose another limitation. Suboptimal parameter choices or deviations from assumed model dynamics may lead to subpar performance or convergence issues. However, conducting sensitivity analysis and careful parameter calibration during algorithm development can mitigate this limitation to a large extent. Additionally, the Gaussian Process Model’s effectiveness relies on the assumption of stationarity in underlying data distributions. In real-world scenarios where renewable energy dynamics exhibit non-stationary behavior, predictive accuracy may be compromised. Techniques such as kernel selection and hyperparameter tuning can enhance the model’s adaptability, but addressing non-stationarity remains a consideration. Moreover, integrating advanced optimization techniques like stochastic dynamic programming introduces additional computational overhead. While these techniques enhance robustness and resilience to uncertainty, they also extend optimization timeframes. However, with careful algorithm design and optimization, these computational demands can be managed effectively without compromising performance. In summary, while the methodology presents several limitations, such as computational complexity and sensitivity to parameter settings, addressing these challenges through careful analysis and algorithmic optimization ensures its continued effectiveness in microgrid management.



